코딩딩딩
[논문리뷰] On the Possibility of Incorporating Cryptocurrency Index into the U.S. ETF Market: From the Perspective of Systemic Risk and Mean-Variance Portfolio Optimization 본문
[논문리뷰] On the Possibility of Incorporating Cryptocurrency Index into the U.S. ETF Market: From the Perspective of Systemic Risk and Mean-Variance Portfolio Optimization
komizke 2024. 7. 22. 06:00* 본글의 사진과 내용은 논문을 바탕으로 작성하였습니다.
1. 서론
ETF((Exchange-Traded Fund))란 코스피, 코스닥과 같은 국가의 주요 지수나
금, 원자재, 통화 등의 자산 가치를 추종하는 투자 상품을 일컫는다.
LP((Liquidity Provider))와 AP((Authorized Participant))에 의해 순자산가치로 수렴하는 특성이 있다.
<추가 개념>
LP: 금융상품의 매매가 원활하게 이루어지도록 매도와 매수 호가를 지속적으로 제시하는 역할 담당.
AP: ETF를 발행하며 환매의 권한을 가진 금융기관
본연구의 목적은 2차 전지, 메타버스, 금, 원유 등 다양한 종류의 ETF가 시장에 상장되는 흐름에서
암호화폐 ETF가 미국 ETF시장에 정착했을 때 효과를 검증하고자 한다.
분석 방법은 아래와 같다.
1) 미국 ETF 시장의 취약성((market vulnerability)) 분석
Kim et al.((2017))에 따르면 2007년 미국에 608개의 ETF가 상장했으며 2016년 12월 기준,
1705개로 증가했으며 고유벡터 3개를 기반으로 계산한 absorption ratio가 0.524에서 0.468로 크게 감소했다.
이를 활용하여 PCA로 absorption ratio를 계산하여 시스템 리스크를 측정한다.
2) 암호화폐 ETF의 자산적 독립성과 투자가치 분석
암호화폐 ETF 도입 이후, 기존 자산들과 대비하여 독립적인 자산으로서의 역할 수행 여부를 확인하고
투자자들에게 효율적인 투자기회를 제공하는지 검증한다.
How?
1. 섹터별 ETF 상관계수 확인.
2. 현대 포트폴리오 이론에 기반하여 암호화폐 지수 도입 이후 포트폴리오의 기대수익률과 위험도 확인.
2. 암호화폐 지수 도입 시 미국 ETF 시장의 시스템 리스크 분석
2.1 이론적 배경
<시장의 시스템 리스크 구하는 방법>
1) 시장에 financial distress 가해질 때, $CoVaR$을 활용하여 system을 구성하는 자산 간의 충격 계산
$CoVaR$((Comovement Value-at-Risk))는 금융기관 혹은 자산 간의 상호연관성과 공동 변동을
고려한 시스템 전반의 위험 평가에 사용된다.
한 금융기관이 위기에 처한 상태에서 다른 금융기관의 $VaR$을 측정하는 방식이다.
특정 회사((i))가 주가수익률이 최대손실예상액((VaR)) 수준에 도달했다는 financail distress 조건 하에서
해당 권역에 속한 타 회사((j))의 주가수익률의 조건부 최대손실예상액이 $CoVaR$이 된다.
<추가 개념>
최대손실예상액((value-at-risk, VaR)): 특정 신뢰수준 하에서 최대 예상 손실 금액
$q$% - VaR : $q$%의 확률로 손실이 특정 금액을 넘지 않는다는 의미
시스템에 포함된 한 회사와 시스템 전체 수익률은 ‘이변량 정규분포’로 가정한다.

위의 식 ((3))에서 $ \bigtriangleup CoVaR_{q}^{j|i}$는 특정회사(i)가
일반 상태일 때와 financial ditress 상태일 때의 타 회사((j))의 $VaR$차이를 의미하고
$\bigtriangleup CoVaR_{q}^{j|i}$ 값이 0에 가까워질수록
특정회사((i))가 재무적 곤경 조건이더라도 타 회사((j))에 미치는 위험이 적어진다.
이를 바탕으로 j를 시스템으로 가정하여 특정기관((i))이 시스템((j))에 미치는 영향을 분석하고자 한다.
시스템에 포함된 한 회사와 시스템 전체의 수익률은 아래와 같은 이변량 정규본포를 따른다고 가정한다.

다변량 정규분포 특성에 의해, 특정기관((i))의 수익률에 대한
시스템 수익률의 조건부 분포는 아래와 같은 정규분포를 따른다.

Mainik and Schaanning((2014)) 은 $\alpha$%- 유의 수준 $(\Phi ^{-1}(\alpha ))$을 가진 시스템과
$\beta$%- 유의 수준 $(\Phi ^{-1}(\beta))$을 가진 시스템에 포함된 회사의 $CoVaR$은 아래와 같이 정의한다.
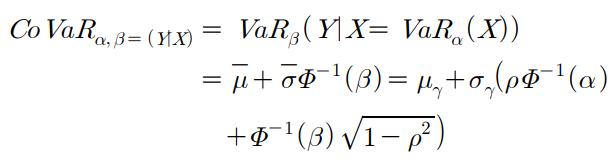
시스템에 포함된 한 기업과 시스템 전체가 $q$%-유의 수준을 가진다고 할 때
$\Delta CoVaR_{q}^{i}$은 아래와 같다.

2) 흡수 비율 활용
$PCA$결과로 나온 주성분을 이용해 리스크가 나온 요인의 집중도인
흡수 비율을 측정한다. ((Kritzman et al.(2011)))
흡수비율이 1에 가까울수록 주가수익률이 적은 수의 위험 인자에 의해
설명되기에 시스템 리스크가 높다고 할 수 있다.

2.2 미국 ETF 시장 데이터 수집 및 방법론
2022년 1월 12일 미국 금융 시장에 상장된 2,164개 ETF와
시총 상위 500개의 암호화폐에 대해 2018년 12월 31일 ~ 2021년 12월 31일 기간에서
종가 데이터를 수집하고 일별 로그 수익률 데이터를 계산한다.
위에서 선정된 암호화폐를 바탕으로 암호화폐 지수를 아래와 같은 방법으로 제작한다.
1. CoinMarketCap의 암호화폐 카테고리 참고하여
위에서 선정한 암호화폐의 비율이 50% 이상인 카테고리만 선정한다.
2. 각 카테고리 포함된 선정된 암호화폐의 개수를 확인하고
그 개수의 평균 이상의 크기가 포함된 카테고리를 다시 선별한다.
3. 암호화폐 시가총액 비중에 따라 암호화폐의 지수를 구성하고
시간에 따른 비중 변화는 고려하지 않고 고정시킨다.
ETF 특성상 특정 지수를 추종하여 유사한 수익률의 움직임을 보이며
암호화폐의 경우 비트코인 수익률을 추종하는 경향이 존재하는 부분에서
비슷한 수익률의 움직임을 가진 ETF들을 군집화하여 분석 대상의 범위를 축소하는 과정을 거친다.
<군집화 방법>
1. ETF수익률 간의 상관관계로 데이터 포인트 간의 유사성 측정.
2. 이를 이용해 K-평균 군집화 시행.
<군집화 성능 판단 지표>
1. 평균 상관관계
각 군집의 중심과 군집 내 자산 간 수익률 상관관계의 평균을 계산한다.
평균값이 1에 가까울수록 군집화 잘 되었음을 나타낸다.
2. 실루엣 계수
a((i)): 해당 데이터 포인트와 같은 군집 안에 있는 다른 데이터 포인트와의 거리를 평균한 값.
b((i)): 해당 데이터가 속하지 않은 군집 중 가장 가까운 군집과의 평균 거리.
a((i))와 b((i))를 기반으로 계산하며 그 값이 1에 가까울수록 군집화가 잘 되었음을 의미한다.

본 연구에서 K-평균 군집화 결과 -> 상관관계: 0.9, 평균 실루엣 계수: 0.678
2.3 결과분석
((1)) $CoVaR$ 분석
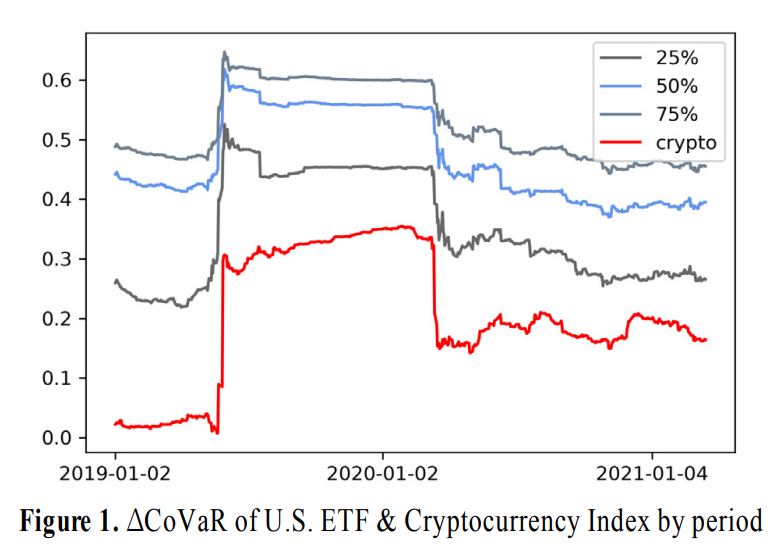
위의 차트에서 보이는 것처럼 암호화폐 지수로 구성된 $\left|\bigtriangleup CoVaR\right|$의 값이
타 ETF의 $\left|\bigtriangleup CoVaR\right|$ 보다 작다.
따라서 암호화폐 지수 군집이 상대적으로 시스템 리스크에 미치는 영향이 적다는 것을 나타낸다.
((2)) 흡수비율((absorption ratio))분석

위의 결과처럼 주성분의 개수를 달리해가며 흡수 비율을 비교했으며,
암호화폐 지수 군집이 포함될 때 흡수 비율의 값이 평균적으로 0.028정도 작았으며
이는 시스템 리스크에 미치는 영향이 더 작다고 말할 수 있다.
또한 암호화폐의 지수 개수가 타 ETF지수의 개수보다 현저히 적음에도 불구하고
이러한 결과 측면에서 미국 ETF시장의 시스템 리스크 관점에서 긍정적인 효과를 불러일으킬 수 있다.
3. 암호화폐 지수 도입 시 미국 ETF 시장의 포트폴리오 분석
3.1 이론적 배경
((1)) Sharpe Ratio
포트폴리오의 기대수익률과 기대위험은 trade-off이다.
Harry M.Markowitz가 제시한 'Portfolio Selection Theory'에 따른
최정요구기대수익률을 만족하면서 기대위험도를 최소화하는 포트폴리오를 구성한다.
포트폴리오 성과 측정 -> Sharpe Ratio((William F. Sharpe)) 사용
Sharpe Ratio의 경우, 실제 금융 시장의 수익률은 정규분포가 아니지만
투자 포트폴리오의 수익률을 정규분포임을 가정하는 부분에서 한계점이 존재하지만,
현대 포트폴리오 이론에서 투자의 위험 대비 수익을 나타내는 가장 대표적인 지수이다.
샤프 지수가 높을수록 해당 시장에서 위함 대비 높은 수익을 얻을 수 있다고 해석할 수 있다.
따라서 암호화폐 ETF가 도입되었을 때
Sharpe ratio 분석을 통해 미국 ETF 시장 도입 가능성을 평가하려고 한다.
하지만 샤프 지수의 값이 절대적인 값이 아니여서 유사한 상품들과 비교가 필요하다.
n개의 자산의 수익률 벡터 $r\hat{I}$, 무위험 수익률 $r_f$,
각각의 자산에 투자하는 포트폴리오 $w\hat{I}$ 존재할 때 Sharpe Ratio는 아래와 같다.
$E(w^{T}r)$, $Std(w^{T}r)$ 는 각각 투자포트폴리오의 기대수익률,
수익률의 표준편차를 나타낸다.

((2)) Sharpe Ratio 비율 최대화 모형
접선 포트폴리오((Tangency Portfolio, TP))란 Sharpe 지수 최대화의 목적함수를 만족시키도록
구성종목들의 보유비중을 결정한 포트폴리오를 의미한다.
그래서 이 지점에서 Sharpe Ratio의 값이 최대가 되어서 위험률 대비 가장 높은 수익률을 얻을 수 있게 된다.
임의의 n개 자산의 수익률 벡터 $r\hat{I}$, 이 수익률 벡터의 평균 $E(r)=m$, 공분산 $Cov(r) = S$,
n개의 자산에 대한 투자 포트폴리오를 $w\hat{I}$이라 할 때,
Sharpe Ratio 최대화하는 자산 배분 결정 문제는 아래와 같다.

하지만 위 식은 컨벡스 최적화 문제에 속하지 않아서 일반해의 최적성을 보장할 수 없다.
그래서 본 연구에서는 Iyengar and Kang ((2005))에 제시된 Sharpe Ratio 최대화 문제에 대한
컨벡스 문제로의 재수식화 결과를 활용했다.
결정변수 $y$는 $n$-차원 실수 벡터이며 수식은 아래와 같다.


((3)) 미국 ETF 종류별 암호화폐 지수와의 상관관계 비교
보통 좋은 투자 대상이라고 하는 것은 기존의 자산군에 대해서 추가로 다각화가 가능하다고 한다.
Chris et al.((2016))에서 기존의 자산군과 새로운 자산의 상관관계의 절댓값이 0에 가까울수록
다각화에 따른 risk 감소 효과가 큰 편이며, 0.5 정도면 적합하다고 주장한다.
3.2 결과 분석
((1)) 미국 ETF섹터별 암호화폐 지수와의 상관관계 비교 결과
미국 ETF에 대해 Investing.com에서 제시하는 섹터 equity, bond, commodity, currency, others로 분류하여
암호화폐까지 포함한 기초 통계량은 아래와 같다.

섹터별 수익률 평균으로 계산한 상관관계 행렬을 아래와 같다.

위의 상관관계 행렬에서 암호화폐 지수는 타 섹터들에 비하여 낮은 상관관계의 값이 나타나는 것으로 보아
다른 ETF의 움직임과 분리되었다고 해석할 수 있다.
((2)) 기간별 상관관계 분석
전체 기간에 대해 상관분석을 하게 될 경우 기간 내 투자환경 변화를 고려하지 못하기에
분산 효과의 변화 추이를 효과적으로 확인하기 어렵다.
따라서 이동창을 통해 연속적인 분산 효과의 변화 추이를 확인한다.
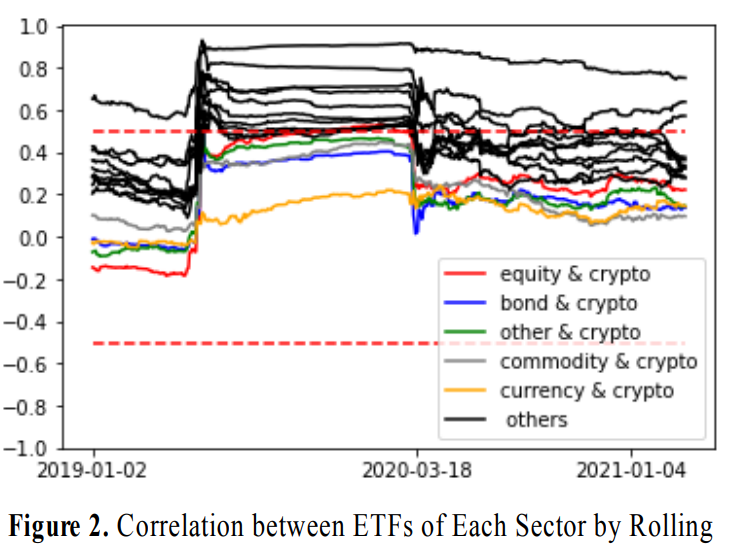
아래 그래프는 200일 간격으로 암호화폐 지수와 타 섹터 ETF의 상관관계를 관찰한 결과이다.
암호화폐 지수들과 타 섹터 ETF들의 상관관계는 대부분 0.5 이하의 값을 나타내며
타 섹터 ETF들 간의 상관관계보다 낮은 상관관계를 보인다.
따라서 암호화폐 지수가 미국 ETF 시장으로 도입이 된다면
새로운 투자 자산으로 제 기능을 하여 시장의 다양성을 높일 것으로 기대된다.
((3)) 효율적 투자선과 Sharpe 비율 분석
One-fund theorm에 따르면, 무위험 자산을 포함하면
기대수익률은 높고 위험도는 낮은 투자 포트폴리오를 만들 수 있다고 한다.
따라서 tangency protfolio를 구할 수 있게 된다.
무위험 수익률은 10년 미국 국고채 수익률인 2.018%로 가정한다.
본 연구에서는 효율적 투자선의 변화를 분석하였으며
자산별 포트폴리오의 비율은 몬테카를로 시뮬레이션 기법을 적용했다.
아래는 효율적 경계선을 시각화한 결과이다.

효율적 경계선 측면에서 암호화폐 도입이 효과가 있는 년도: 2019, 2020
Sharpe Ratio 측면에서 암호화폐 도입이 효과가 있는 년도: 2020
전체 분석 기간에 대해서 Sarpe Ratio 측면과 효율적 경계선 측면에서 효과가 있는 것으로 나타난다.
4. 결론
본 연구는 가상의 암호화폐 ETF를 미국 시장에 도입하여
시스템 리스크와 포트폴리오 관점에서 비교하여 도입 가능성까지 분석하였다.
$CoVaR$과 absorption ratio의 값 모두 암호화폐 지수를 포함한 시스템에서 긍정적인 결과를 보였다.
암호화폐 지수의 도입은 기대수익률과 위험도 측면에서도 효율적인 투자 기회를 제공한다.
본 연구에서 사용한 암호화폐 ETF 생성 방법과 다른 암호화폐 기반 기술, 시가총액 등 다양한 방식으로
접근하여 금융시장에 도입하기 좋은 ETF를 선별하여 암호화폐 ETF도입으로부터의 효과가 커지길 기대한다.




